最小二乘法线性回归：矩阵视角

这篇文章将会用矩阵微积分和几何的视角来介绍最小二乘法线性回归（OLS），我想尽量直观地展现最小二乘法线性回归的合理、美妙之处，有一点线性代数知识可以帮助理解，没学过线性代数了解一下对以后的学习也有帮助。

思想

线性回归的思想来自于 Francis Galton 在 1863 年发现的均值回归现象。Galton 在研究父母与孩子身高的关系时发现，$\text{孩子的身高} = \text{人口平均身高} \times w_0 + \text{父母身高} \times w_1$，也是说如果小李父母很高，平均 2 米 1，小李不太可能比他的父母高，身高会向人口均值靠拢，小程父母很矮，平均 1 米 4，小程不太可能比他的父母矮，身高也会向人口均值靠拢。

诺贝尔经济学奖获得者 Daniel Kahneman 讲述过他最满意的 "Eureka moment" 是他意外发现均值回归可以用来解释为什么驾校教练特别喜欢责骂学员而不是表扬学员。因为如果学员这次表现好，远超平均水平，这时候教练表扬学员，教练会发现下次学员的表现变差了；如果学员这次表现很差，低于平均水平，这时候教练责骂学员，教练会发现下次学员的表现变好了。因此教练得出结论：责骂比表扬更有用。然而实际上，学员表现变好或者变差都是均值回归现象而已。

可惜 Galton 并没有把回归发扬光大，George Udny Yule 继承其思想并用最小二乘法估计权重系数，用于研究救济金是否导致贫穷，直到今天我们依然在延续着「回归均值」的思想。

极大似然估计和最小二乘法

最小二乘法线性回归作为最基础的线性回归，在统计和机器学习中都有重要戏份，至于线性回归的深入研究，各领域因为研究的问题不同而分道扬镳。在统计和计量经济学中，线性回归用来检验因果关系，因此结果的分布、如何检验结果的显著性、数据不符合假设如何处理是主要的研究问题。在机器学习里，线性回归用来从数据中获得启示来帮助预测，因此如何得到最拟合数据的函数和防止过拟合是研究重点。

以估计房价为例，假设真实世界里房子的面积 $x$ 与房价 $y$ 的关系是线性关系，且真实世界存在无法估计的误差 $\epsilon$，也就是 $y = w_0 + w_1x + \epsilon$，不管是为了机器学习里的预测，还是为了计量经济学里检验面积重不重要，我们都要估计出 $w_0$ 和 $w_1$ 的值。在统计学，这个系数称为参数，用 $\beta$ 表示。在可预期的未来，我悲观地认为机器学习和统计学不太可能统一符号和语言，学数学的一部分就是学习与不同的数学符号相处，这里我使用 $w$ 是因为我认为 $w$ 代表权重（weight）更为直观，并不代表我是经济学生里的叛徒呜呜呜。

可能有不止一个因素影响房价 $y$，房子的面积、卧室的数量等等，设房子的面积 $x_1$，卧室的数量 $x_2$，这样模型就是 $y = w_0 + w_1x_1 + w_2x_2 + \epsilon$，这时候我们就需要估计 $w_0$，$w_1$ 和 $w_2$ 的值。

为了估计各项 $w$ 的值，有多种方法，频率学派的最小二乘法和极大似然估计，贝叶斯学派的最大后验估计等等。最容易理解的是最小二乘法，找到使误差 $\epsilon$ 的平方和最小 $w_0$，$w_1$ 和 $w_2$ 即可。

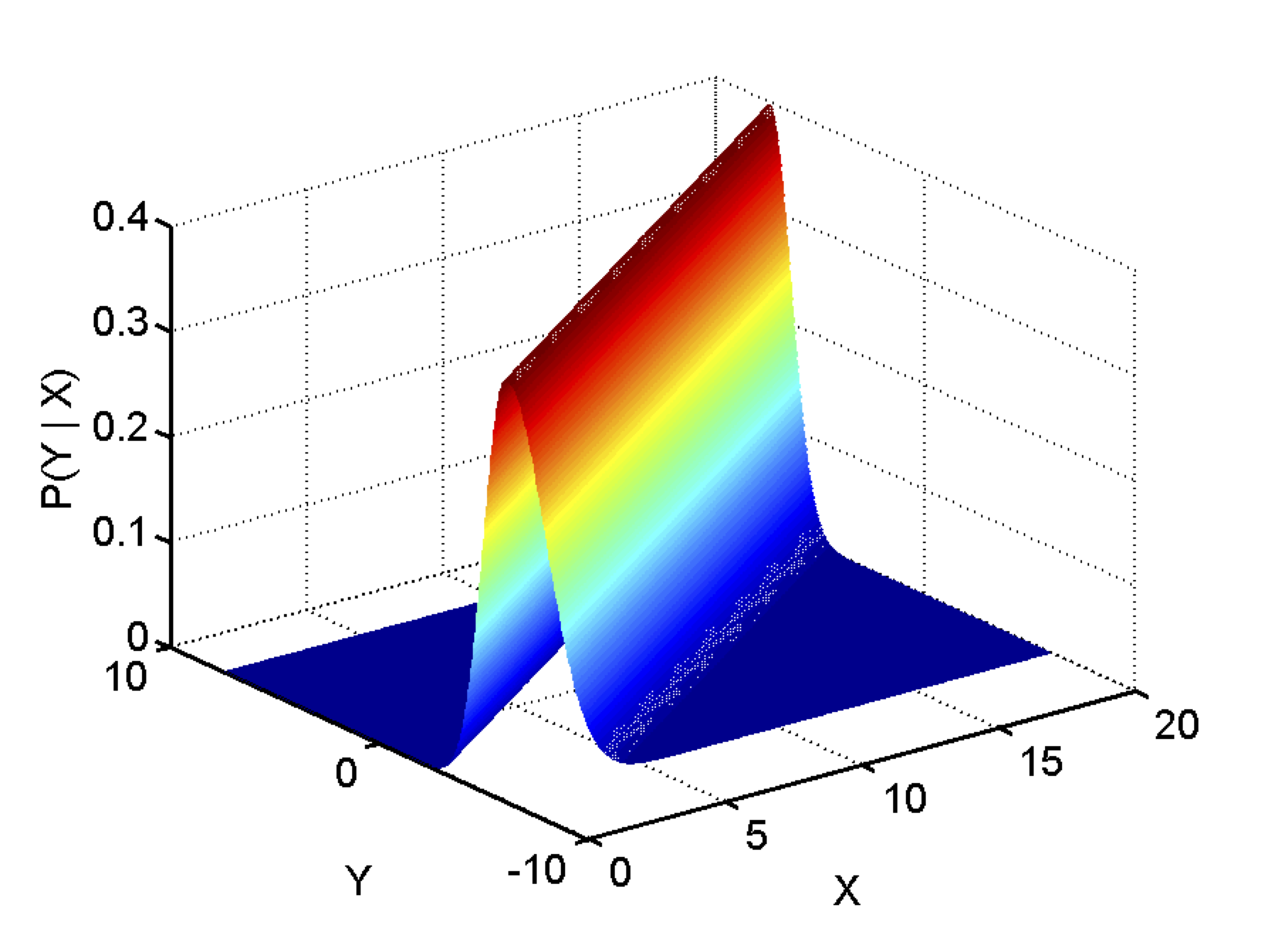
其次好理解的是极大似然估计，假设误差服从某个分布，找到让我们最有可能获得已有数据的 $w_0$，$w_1$ 和 $w_2$ ，也就是使 $P(\text{已有数据} \mid w_0,w_1,w_2)$ 最大的 $w_0$，$w_1$ 和 $w_2$。如果我们假设误差服从正态分布，如上图所示，数据是独立同分布（i.i.d.），最小二乘法得出的 $w_0$，$w_1$ 和 $w_2$ 就是极大似然估计。

不要觉得最小二乘法想法简单所以没用，我也有过这样的错误想法。1809 年高斯用最小二乘法估计出了谷神星的轨道，在此之后高斯为了最小二乘法发明者的头衔和 Legendre 争论不休，1829 年高斯证明了最小二乘法有特别好的性质，也就是高斯－马尔可夫定理，得再写一篇文章才能讲清楚。

有了收集好的数据，就可以用矩阵和微积分来得到权重。这些收集到的数据有很多条，用下标表示数据条目，这里以收集到 5 条数据为例。 $$y_1 = w_0 + w_1x_{11} + w_2x_{12} + \epsilon_1$$ $$y_2 = w_0 + w_1x_{21} + w_2x_{22} + \epsilon_2$$ $$y_3 = w_0 + w_1x_{31} + w_2x_{32} + \epsilon_3$$ $$y_4 = w_0 + w_1x_{41} + w_2x_{42} + \epsilon_4$$ $$y_5 = w_0 + w_1x_{51} + w_2x_{52} + \epsilon_5$$

看起来很混乱？是的，所以我们需要使用矩阵来简化这些繁琐的等式。 $$ \overrightarrow{y} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{bmatrix},\quad X = \begin{bmatrix} 1 & x_{11} & x_{12} \\ 1 & x_{21} & x_{22} \\ 1 & x_{31} & x_{32} \\ 1 & x_{41} & x_{42} \\ 1 & x_{51} & x_{52} \end{bmatrix},\quad \overrightarrow{w} = \begin{bmatrix} w_0 \\ w_1 \\ w_2 \end{bmatrix},\quad \overrightarrow{\epsilon} = \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \end{bmatrix} $$

用矩阵乘法，就可以得到上面繁杂等式的简化版本。 $$\overrightarrow{y} = X\overrightarrow{w} + \overrightarrow{\epsilon}$$

最小二乘法的思想就是找到 $\overrightarrow{w}$ 让 $\overrightarrow{\epsilon}$ 的平方和，$\overrightarrow{\epsilon}^T\overrightarrow{\epsilon}$最小。为了简化公式，我这里不再使用箭头表示向量，而用小写字母表示列向量，大写表示矩阵，表示为 $$ \underset{w}{min} \quad \epsilon^{T}\epsilon$$

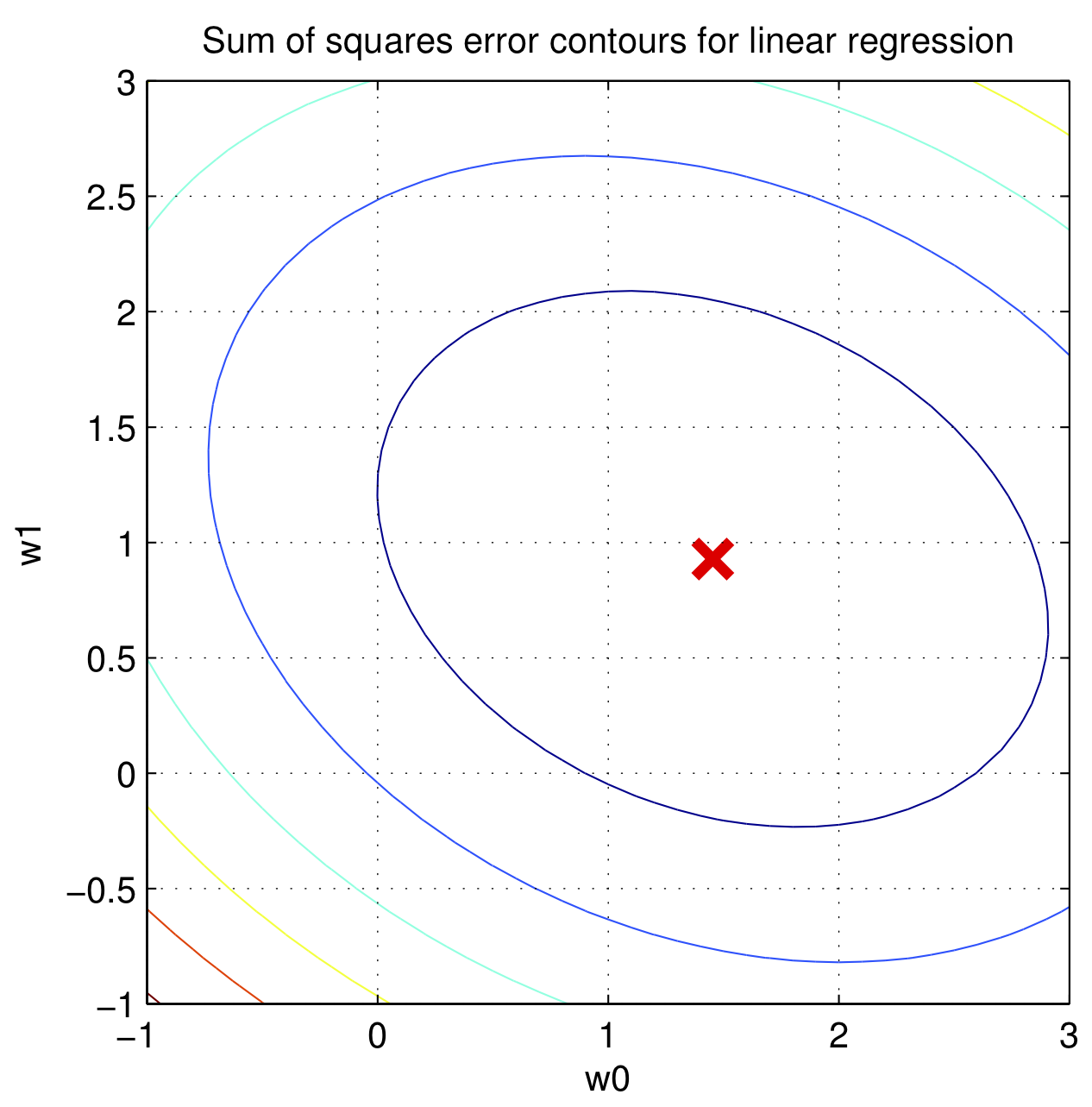
如果 $\overrightarrow{w}$ 是二维的，$\epsilon^{T}\epsilon$ 的图像是一个碗，如上图所示，这意味着存在一个全局最低点，这样的函数叫做凸函数，可以使用梯度下降法来得到全局最低点对应的的 $\overrightarrow{w}$，这个方法在吴恩达的机器学习里有详细描述，鄙人也在博客里作过拙文机器学习中的梯度下降法，这里不再赘述，只讲用微积分直接求解。

由于 $\epsilon = y - Xw$, $(AB)^T = B^TA^T$ 以及矩阵代数符合乘法分配律，我们可以打开平方和得到 $$ \begin{equation} \begin{split} \epsilon^{T}\epsilon & = (y - Xw)^T(y - Xw)\\ & = (y - Xw)^Ty - (y - Xw)^TXw \\ & = y^Ty - (Xw)^Ty - y^TXw + (Xw)^TXw \\ & = y^Ty - w^TX^Ty - y^TXw + w^TX^TXw \end{split} \end{equation} $$

$w^TX^Ty$ 和 $y^TXw$ 得到的结果都是 $1\times1$ 的标量，对于标量 $a$，$a^T = a$，因此 $w^TX^Ty = (w^TX^Ty)^T = y^TXw$。

$$ \begin{equation} \label{rss} \begin{split} \epsilon^{T}\epsilon & = y^Ty - (Xw)^Ty - y^TXw + (Xw)^TXw \\ & = y^Ty - 2w^TX^Ty + w^TX^TXw \end{split} \end{equation} $$

让 $\epsilon^{T}\epsilon$ 的梯度为零就可得到最小值，梯度就是导数的标量、向量或者矩阵形式。对于将一维标量映射到一维标量的函数，例如 $f(x)=2x$，其梯度是标量，就是导数 $f'(x)=2$，$\epsilon^{T}\epsilon$ 是一个将三维向量 $w$ 映射到一维标量的函数，其梯度为向量，将多维向量映射到多维向量的函数，其梯度为矩阵。用倒三角 $\nabla$ 表示梯度，对于 $\epsilon^{T}\epsilon$ 的梯度我们定义为 $$\nabla_{w}\epsilon^{T}\epsilon = \begin{bmatrix} \frac{\partial \epsilon^{T}\epsilon}{\partial w_0}\\ \frac{\partial \epsilon^{T}\epsilon}{\partial w_1}\\ \frac{\partial \epsilon^{T}\epsilon}{\partial w_2} \end{bmatrix}$$

我们先看 $\nabla_{w}w^Ta$ 的情况， $a = \begin{bmatrix} a_0\\ a_1\\ a_2 \end{bmatrix}$， 用标量形式表示就是 $w^Ta = w_0a_0 + w_1a_1+w_2a_2$，可得

$$\nabla_{w}w^Ta = \begin{bmatrix} \frac{\partial w^Ta}{\partial w_0}\\ \frac{\partial w^Ta}{\partial w_1}\\ \frac{\partial w^Ta}{\partial w_2} \end{bmatrix} = \begin{bmatrix} a_0\\ a_1\\ a_2 \end{bmatrix} = a $$

因此可得 $\epsilon^{T}\epsilon$ 中的 $- 2w^TX^Ty$ 的梯度是 $-2X^Ty$。

对于 $\nabla_{w}w^TAw$，$A$ 必须为对称矩阵， $A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{bmatrix}$，可得

$$ \begin{equation} \begin{split} w^TAw &= \begin{bmatrix}w_0 & w_1 & w_2\end{bmatrix}\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{bmatrix}\begin{bmatrix} w_0 \\ w_1 \\ w_2 \end{bmatrix} \\ & = \begin{bmatrix}w_0 & w_1 & w_2\end{bmatrix} \begin{bmatrix} a_{11}w_0 + a_{12}w_1 + a_{13}w_2 \\ a_{12}w_0 + a_{22}w_1 + a_{23}w_2 \\ a_{13}w_0 + a_{23}w_1 + a_{33}w_2 \end{bmatrix} \\ & = \quad w_0(a_{11}w_0 + a_{12}w_1 + a_{13}w_2)\\ & \quad +w_1(a_{12}w_0 + a_{22}w_1 + a_{23}w_2)\\ & \quad +w_2(a_{13}w_0 + a_{23}w_1 + a_{33}w_2) \\ & = a_{11}w_0^2+ a_{22}w_1^2 + a_{33}w_2^2 +2a_{12}w_0w_1+ 2a_{13}w_0w_2+2a_{23}w_1w_2 \end{split} \end{equation} $$

因此 $$ \nabla_{w}w^TAw = \begin{bmatrix} \frac{\partial w^TAw}{\partial w_0}\\ \frac{\partial w^TAw}{\partial w_1}\\ \frac{\partial w^TAw}{\partial w_2} \end{bmatrix} = \begin{bmatrix} 2a_{11}w_0 + 2a_{12}w_1 + 2a_{13}w_2\\ 2a_{12}w_0 + 2a_{22}w_1 + 2a_{23}w_2\\ 2a_{13}w_0 + 2a_{23}w_1 + 2a_{33}w_2 \end{bmatrix} = 2Aw $$

对于 $\epsilon^{T}\epsilon$ 中的 $w^TX^TXw$, 无论有多少条数据，$X^TX$ 都是 $3\times3$ 的对称矩阵（太美妙了！），因此可得 $w^TX^TXw$ 的梯度是 $2X^TX$。

由以上推导可得梯度 $$\nabla_{w}\epsilon^{T}\epsilon = \begin{bmatrix} \frac{\partial \epsilon^{T}\epsilon}{\partial w_0}\\ \frac{\partial \epsilon^{T}\epsilon}{\partial w_1}\\ \frac{\partial \epsilon^{T}\epsilon}{\partial w_2} \end{bmatrix} = 2X^TXw - 2X^Ty $$

当 $\epsilon^{T}\epsilon$ 最小时梯度为 0 ，梯度上的各项偏导数为 0，由此可得该位置的 $\hat{w}$ $$\begin{equation} \begin{split} 2X^TX \hat{w} - 2X^Ty & = 0 \\ X^TX \hat{w} & = X^Ty \\ \hat{w} &= (X^TX)^{-1}X^Ty \end{split} \end{equation}$$

以上对矩阵微积分进行的推导因为追求直观所以并不严谨，用求和符号 $\Sigma$ 也可以推出相同的结论，可参见斯坦福 CS231n 的附录 Vector, Matrix, and Tensor Derivatives 和 fast.ai 的 The Matrix Calculus You Need For Deep Learning。

贝叶斯学派视角下的线性回归是完全不同的视角，鄙人不才没法讨论清楚。贝叶斯线性回归在特定条件下可以得到和极大似然估计/最小二乘法相同的分布，但极大似然估计/最小二乘法要求$\text{数据条目数}\ n \geq \text{数据特征数}\ d + 1$，$X$ 中的各向量线性无关 (linearly independent)，这样 $X^TX$ 才有逆矩阵，而贝叶斯线性回归没有这样的要求。直观的理解是如果我们至少要有 2 个不同的点，才能在二维平面拟合一条直线，至少要有 3 个不共线的点，才能在三维空间里拟合一个平面。这里我们有 5 条数据和 2 项特征，$5 > 2+1$，因此可以使用极大似然估计/最小二乘法。

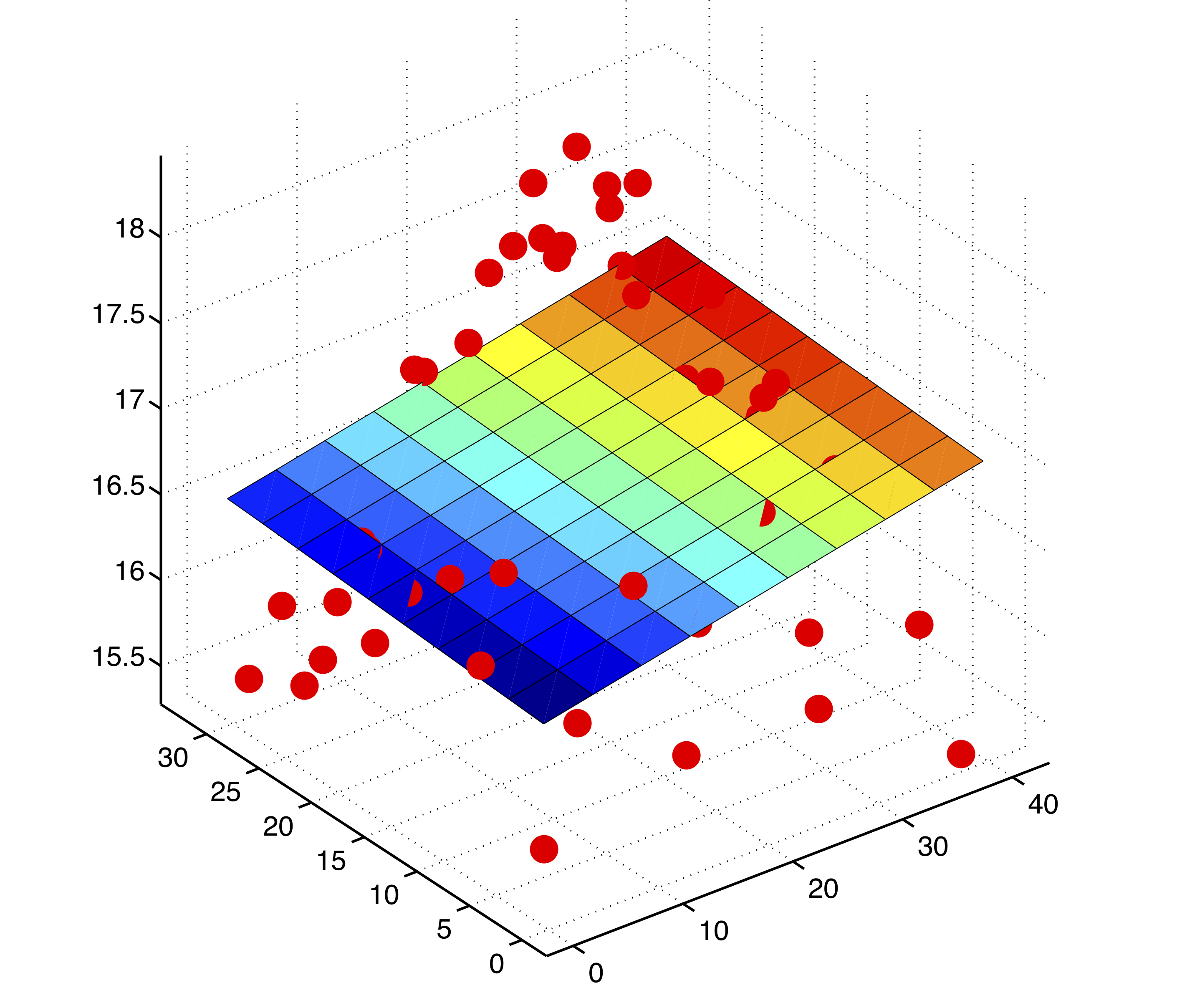
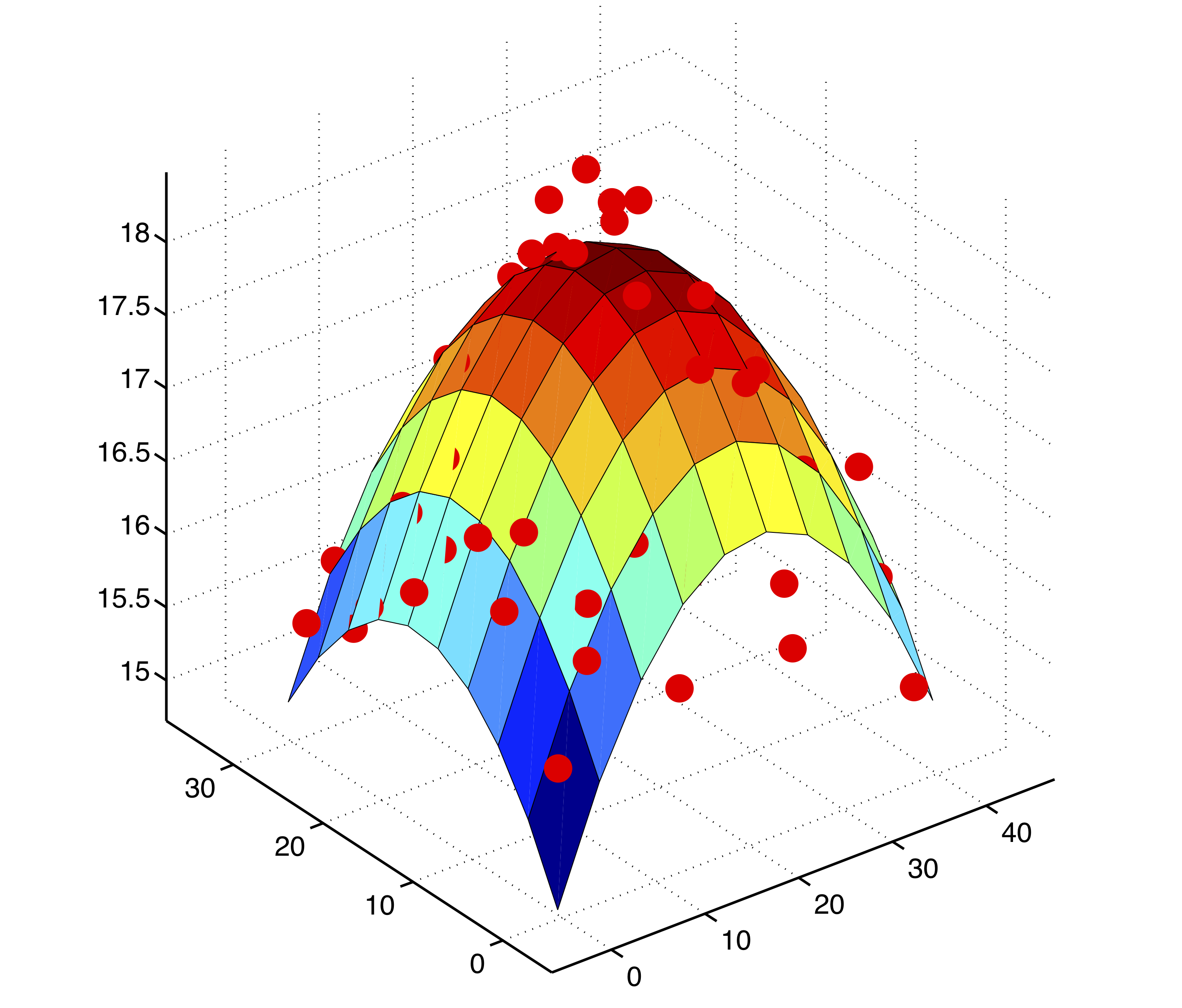
特征的 n 次方也有可能对 $y$ 有影响。机器学习的方法是把 $X$ 转换为 $\phi(X)$，例如 $$ X = \begin{bmatrix} 1 & x_{11} & x_{12} \\ 1 & x_{21} & x_{22} \\ 1 & x_{31} & x_{32} \\ 1 & x_{41} & x_{42} \\ 1 & x_{51} & x_{52} \end{bmatrix} \rightarrow \phi(X) = \begin{bmatrix} 1 & x_{11} & x_{12} & x_{11}^2 & x_{12}^2 \\ 1 & x_{21} & x_{22} & x_{21}^2 & x_{22}^2 \\ 1 & x_{31} & x_{32} & x_{31}^2 & x_{32}^2 \\ 1 & x_{41} & x_{42} & x_{41}^2 & x_{42}^2 \\ 1 & x_{51} & x_{52} & x_{51}^2 & x_{52}^2 \end{bmatrix} $$

然后使用最小二乘法得到相应的权重，形成曲面（高维空间在三维空间的投影），如上图所示，称为多项式回归。在计量经济学上，则是检验 $y = X\beta_1 + \hat{y}^2\beta_2 +\epsilon$ 中的 $\beta_2$ 是否显著，称为 RESET 检验。

投影矩阵

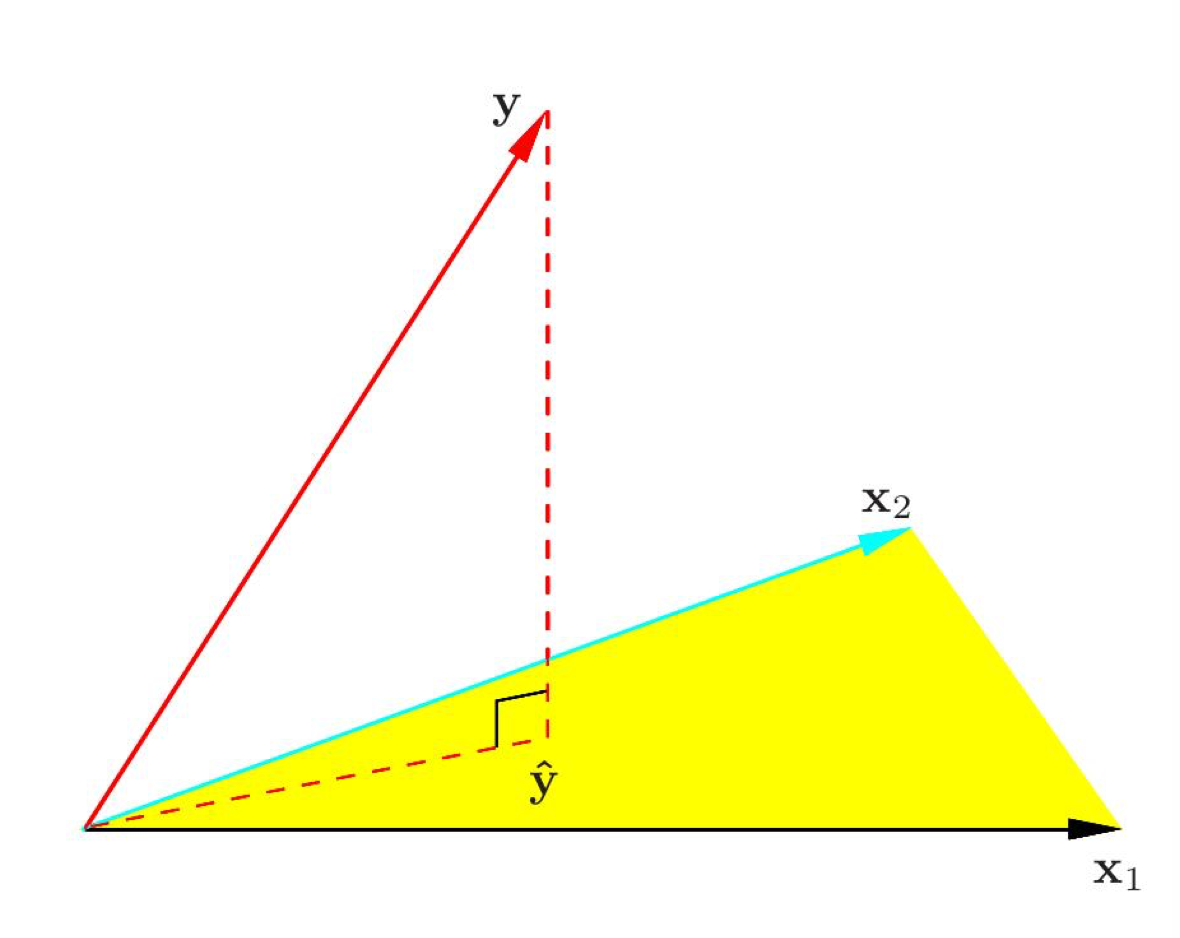
假设我们通过一个特征来估计 $y$，依然有 5 条数据，$X =\begin{bmatrix} 1 & x_{11}\\ 1 & x_{21}\\ 1 & x_{31}\\ 1 & x_{41}\\ 1 & x_{51} \end{bmatrix}$，$X$ 的两条列向量 $x_1 = \begin{bmatrix} 1\\ 1\\ 1\\ 1\\ 1 \end{bmatrix}$ 和 $x_2= \begin{bmatrix} x_{11}\\ x_{21}\\ x_{31}\\ x_{41}\\ x_{51} \end{bmatrix}$ 通过权重 $w = \begin{bmatrix} w_{1}\\ w_{2} \end{bmatrix}$ 张成了 2 维的子空间，也就是一个平面，我们还知道向量 $y$。因为误差，$y$ 不在 $x_1$ 和 $x_2$ 张成的平面上，怎么样才能找到最好的 $w$ 呢？ 一种答案是找到 $y$ 在 $x_1$ 和 $x_2$ 张成的平面上投影 $\hat{y} = X\hat{w}$，如上图所示，$\hat{w}$ 就是最好的 $w$。

由投影的性质可知 $y - \hat{y}$ 垂直于 $x_1$ 和 $x_2$，用人话说就是从 $\hat{y}$ 的终点到 $y$ 的终点是一条垂直于 $x_1$ 和 $x_2$ 的向量，可得

$$ (y - \hat{y})^Tx_1 = (y - X\hat{w})^Tx_1 = 0\\ (y - \hat{y})^Tx_2 = (y - X\hat{w})^Tx_2 = 0 $$

把上式合并，可得

$$ \begin{equation} \begin{split} (y-X\hat{w})^TX &= 0\\ X^T(y-X\hat{w}) &= 0\\ X^Ty-X^TX\hat{w} &= 0\\ X^TX\hat{w} &= X^Ty\\ \hat{w} &= (X^TX)^{-1}X^Ty \end{split} \end{equation} $$

最小二乘法和投影矩阵是两种完全不同的思路，却得到了相同结论，究其原因，投影使 $\hat{y}$ 与 $y$ 的欧式距离最短，这与最小二乘法让误差项平方和最小的思想不谋而合，岂不妙哉？

参考来源

回归均值的历史和讨论参考了 Joshua D. Angrist 和 Jörn-Steffen Pischke 的 Mostly harmless econometrics: An empiricist’s companion p.80。

Daniel Kahneman 的 "Eureka moment" 参考了维基百科的 Regression toward the mean，第一次听说是 CS109 Joe Blitzstein 讲授的 Bias and Regression。

高斯和最小二乘法的历史参考了维基百科的最小二乘法。

线性回归模型里，正态分布和独立同分布（i.i.d.）下的极大似然估计等价于最小二乘法，引自 Kevin Murphy 的 Machine learning: a probabilistic perspective p.218。

极大似然估计和贝叶斯线性回归得出相同分布，引自 Kevin Murphy 的 Machine learning: a probabilistic perspective p.237。

投影矩阵的性质参考了 Gilbert Strang 的 Linear Algebra。

本文大部分图片引自 Kevin Murphy 的 Machine learning: a probabilistic perspective 的图表和 John W. Paisley 在 edx 开设的 Machine Learning。

修改与勘误

• 修改了最后一段结论。
• $X^TX$ 的逆矩阵存在需要两个条件，1. 线性无关 2. 行数 > 列数，因此修改了文章对 $(X^TX)^{-1}$ 存在的条件和直觉上的理解。