最小二乘法的利与弊:高斯马尔科夫定理¶
作者:李家伟
在《最小二乘法线性回归:矩阵视角》 一文里,我提到高斯马尔科夫定理证明了最小二乘法线性回归(OLS,下同)有一些特别好的性质,具体来说,当误差项均值为 0 时,OLS 得到的 $w$ 无偏(unbiased),如果各误差项方差相同,OLS 得到的 $w$ 是最佳无偏线性估计(BLUE, best linear unbiased estimator)。这篇文章里我会解释什么是无偏、什么是最佳无偏线性估计、如何证明 OLS 具有这些性质,并由此展开讨论 OLS 的局限。
如何评价 OLS?¶
在评价 OLS 之前,我们先定义评价的标准,什么是好的估计?这里我们采用频率学派的标准,即偏差(Bias)和方差(Variance)。
真实的数值表示为 $w$,我们基于样本估计出的数值表示为 $\hat{w}$。由于存在误差 $\epsilon$,$\epsilon$ 是随机变量,影响了 $y$,因此 $y$ 是随机变量,并影响了通过数据估计得到的 $\hat{w}$,在 OLS 中 $\hat{w} = (X^TX)^{-1}X^Ty$,因此 $\hat{w}$ 是随机变量,并有对应的分布。
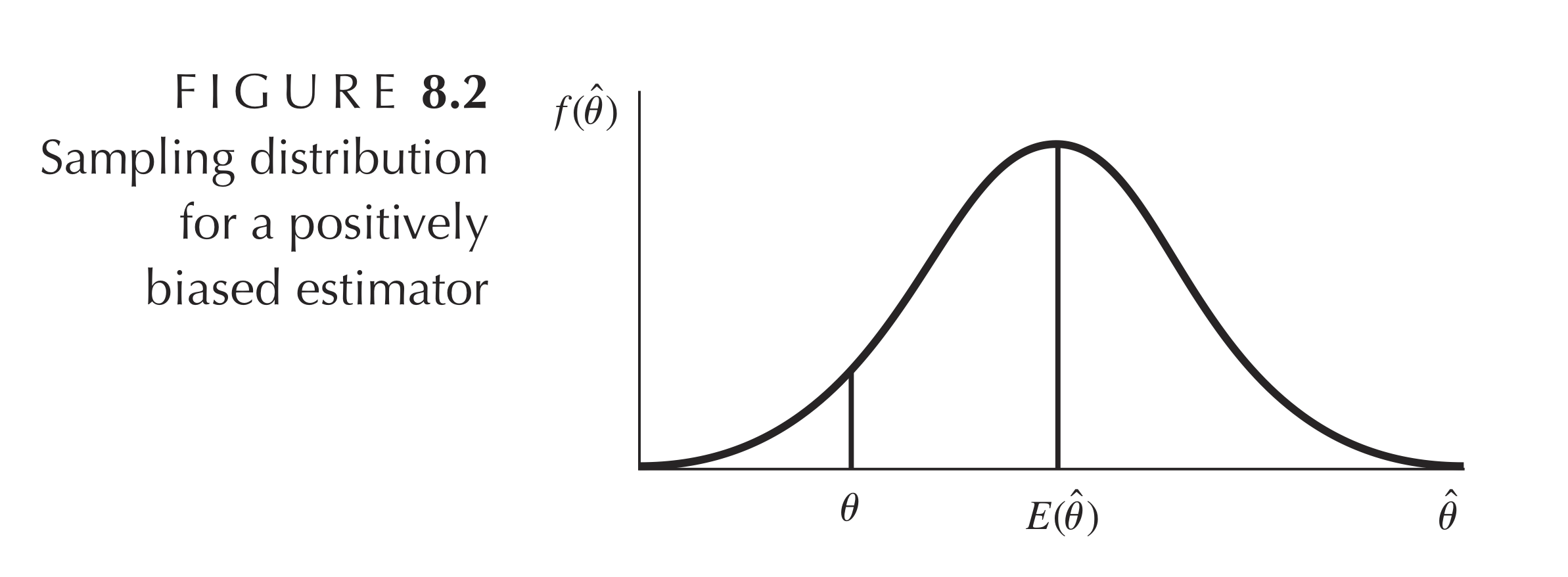
我们希望 $\hat{w}$ 的均值接近 $w$,也就是偏差 $\mathrm{E}(\hat{w}) - w$ 尽量小,当 $\mathrm{E}(\hat{w}) = w$ 时,$\hat{w}$ 就是无偏(Unbiased)估计。如上图所示,当 $\mathrm{E}(\hat{\theta}) \neq \theta$ 时,$\hat{\theta}$ 是有偏(Biased)估计。
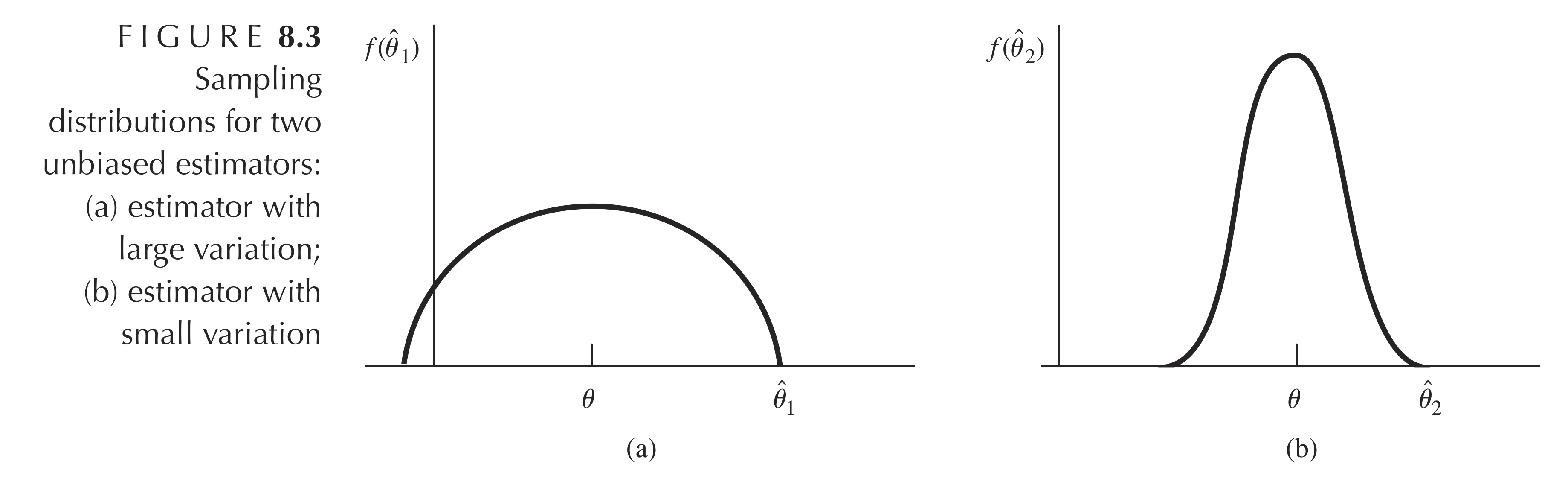
我们希望 $\hat{w}$ 给出的结果 波动小,也就是方差 $\mathrm{Var}(\hat{w})$ 尽量小,如上图所示,我们想要方差更小的 (b)。如果 $\mathrm{Var}(\hat{w})$ 是所有估计里最小的,$\hat{w}$ 就是最佳估计。如果 $\mathrm{Var}(\hat{w})$ 是所有无偏线性估计里最小的,$\hat{w}$ 就是最佳无偏线性估计(BLUE, best linear unbiased estimator)。
期望、协方差¶
沿用《最小二乘法线性回归:矩阵视角》 一文的符号,列向量 $w$ 的期望定义为
$$ w = \begin{bmatrix} w_0 \\ w_1 \\ w_2 \end{bmatrix} ,\quad \mathrm{E}(w) = \begin{bmatrix} \mathrm{E}(w_0) \\ \mathrm{E}(w_1) \\ \mathrm{E}(w_2) \end{bmatrix}=\begin{bmatrix} \bar{w_0} \\ \bar{w_1} \\ \bar{w_2} \end{bmatrix} $$
协方差矩阵是方差以及协方差的矩阵形式,$w$ 的协方差矩阵定义为
$$ \begin{equation} \begin{split} \mathrm{Var}(w) &= \mathrm{E}\big[ [w - \mathrm{E}(w)][w - \mathrm{E}(w)]^T \big]\\ &= \mathrm{E}\Bigg[ \begin{pmatrix} w_0 - \bar{w_0} \\ w_1 - \bar{w_1} \\ w_2 - \bar{w_2} \end{pmatrix} \begin{pmatrix} w_0 - \bar{w_0} & w_1 - \bar{w_1} & w_2 - \bar{w_2} \end{pmatrix} \Bigg]\\ &=\begin{bmatrix} \mathrm{E}[(w_0 - \bar{w_0})(w_0 - \bar{w_0})] & \mathrm{E}[(w_0 - \bar{w_0})(w_1 - \bar{w_1})] & \mathrm{E}[(w_0 - \bar{w_0})(w_2 - \bar{w_2})] \\ \mathrm{E}[(w_1 - \bar{w_1})(w_0 - \bar{w_0})] & \mathrm{E}[(w_1 - \bar{w_1})(w_1 - \bar{w_1})] & \mathrm{E}[(w_1 - \bar{w_1})(w_2 - \bar{w_2})] \\ \mathrm{E}[(w_2 - \bar{w_2})(w_0 - \bar{w_0})] & \mathrm{E}[(w_2 - \bar{w_2})(w_1 - \bar{w_1})] & \mathrm{E}[(w_2 - \bar{w_2})(w_2 - \bar{w_2})] \end{bmatrix} \\ &= \begin{bmatrix} \mathrm{Var}(w_0) & \mathrm{Cov}(w_0 , w_1) & \mathrm{Cov}(w_0 , w_2) \\ \mathrm{Cov}(w_0 , w_1) & \mathrm{Var}(w_1) & \mathrm{Cov}(w_1 , w_2) \\ \mathrm{Cov}(w_0 , w_2) & \mathrm{Cov}(w_1 , w_2) & \mathrm{Var}(w_2) \\ \end{bmatrix} \end{split} \end{equation} $$
我们知道期望和协方差具有以下性质
$$ \begin{equation} \begin{split} \mathrm{E}(A+B) &= \mathrm{E}(A) +\mathrm{E}(B)\\ \mathrm{E}(A^2) &= \mathrm{E}(A)^2 + \mathrm{Var}(A) = \mu^2+\sigma^2\\ \mathrm{Cov}(A,B) &= \mathrm{E}(AB) - \mathrm{E}(A)\mathrm{E}(B)\\ \mathrm{Cov}(A,B) &= 0 \quad 当且仅当\ A,B \ 相互独立 \\ \end{split} \end{equation} $$
$\hat{w}$ 的期望¶
假设真实存在 $y = Xw + \epsilon$, 这里的 $w$ 是个确定值,因此 $\mathrm{E}[w]=w$,通过最小二乘法估计得出 $\hat{w} = (X^TX)^{-1}X^Ty$,这里的 $\hat{w}$ 是随机变量,因此
$$ \begin{equation} \begin{split} \mathrm{E}(\hat{w}) &= \mathrm{E}[(X^TX)^{-1}X^Ty] \\ &= \mathrm{E}[(X^TX)^{-1}X^T(Xw + \epsilon)] \\ &= \mathrm{E}[(X^TX)^{-1}X^TXw] + \mathrm{E}[(X^TX)^{-1}X^T\epsilon] \Longleftarrow (X^TX)^{-1}X^TX = I\\ &= \mathrm{E}[w] + \mathrm{E}[(X^TX)^{-1}X^T\epsilon] \end{split} \end{equation} $$
此时我们引入假设 1:$\mathrm{E}(\epsilon) = 0$,假设 2:$X$ 为确定值(文末会讨论这个假设),$\mathrm{E}(X\epsilon)=X\mathrm{E}(\epsilon) = 0$,可得
$$ \begin{equation} \begin{split} E(\hat{w}) &= \mathrm{E}[w] + \mathrm{E}[(X^TX)^{-1}X^T\epsilon] \\ &= \mathrm{E}[w] + 0 \\ &= w \\ \end{split} \end{equation} $$
由上可得,当 $\mathrm{E}(\epsilon) = 0$ 时,$\mathrm{E}[\hat{w}] = w$,最小二乘法得到的 $\hat{w}$ 无偏(unbiased)。
$\hat{w}$ 的协方差矩阵¶
将 $y = Xw + \epsilon$ 代入 $\hat{w}$ ,得
$$\begin{equation} \begin{split} \hat{w} &= (X^TX)^{-1}X^Ty \\ &= (X^TX)^{-1}X^T(Xw + \epsilon) \\ &= (X^TX)^{-1}X^TXw + (X^TX)^{-1}X^T\epsilon \\ &= w + (X^TX)^{-1}X^T\epsilon \end{split} \end{equation}$$
由于 $E(\hat{w}) = w$,可得协方差矩阵
$$ \begin{equation} \begin{split} \mathrm{Var}(\hat{w}) &= \mathrm{E}\big[ [\hat{w} - \mathrm{E}(\hat{w})][\hat{w} - \mathrm{E}(\hat{w})]^T \big]\\ &= \mathrm{E}\big[ (\hat{w} - w)(\hat{w} - w)^T \big] \end{split} \end{equation} $$
代入 $\hat{w} = w + (X^TX)^{-1}X^T\epsilon$,得
$$ \begin{equation} \begin{split} \mathrm{Var}(\hat{w}) &= \mathrm{E}\big[ (\hat{w} - w)(\hat{w} - w)^T \big] \\ &= \mathrm{E}\big[ [w + (X^TX)^{-1}X^T\epsilon - w][w + (X^TX)^{-1}X^T\epsilon - w]^T \big] \\ &= \mathrm{E}\big[ [(X^TX)^{-1}X^T\epsilon][(X^TX)^{-1}X^T\epsilon]^T \big] \\ &= \mathrm{E}\big[ (X^TX)^{-1}X^T\epsilon\epsilon^T X(X^TX)^{-1} \big] \end{split} \end{equation} $$
因为 $\mathrm{E}(\epsilon) = 0$,可得
$$ \begin{equation} \begin{split} \mathrm{Var}(\epsilon) &= \mathrm{E}\big[ [\epsilon - \mathrm{E}(\epsilon)][\epsilon - \mathrm{E}(\epsilon)]^T \big]\\ &= \mathrm{E}(\epsilon\epsilon^T) \\ & = \begin{bmatrix} \mathrm{E}(\epsilon_1^2) & \mathrm{E}(\epsilon_1\epsilon_2) & \dots& \mathrm{E}(\epsilon_1\epsilon_i)\\ \mathrm{E}(\epsilon_2\epsilon_1) & \mathrm{E}(\epsilon_2^2) & \dots& \mathrm{E}(\epsilon_2\epsilon_i)\\ \vdots & \vdots & \ddots& \vdots\\ \mathrm{E}(\epsilon_i\epsilon_1) & \mathrm{E}(\epsilon_i\epsilon_2) & \dots& \mathrm{E}(\epsilon_i^2)\\ \end{bmatrix} \end{split} \end{equation} $$
现在我们需要引入假设 3.1:任意项 $\epsilon_i$ 与 $\epsilon_j$ 独立,因此 $\forall i \neq j,\ \mathrm{Cov}(\epsilon_{i},\epsilon_j)=\mathrm{E}(\epsilon_i\epsilon_j)=\mathrm{E}(\epsilon_i)\mathrm{E}(\epsilon_j)=0$。
对角线上的 $\mathrm{E}(\epsilon_j^2) = \mathrm{Var}(\epsilon_j) $,引入假设 3.2:任意项 $\mathrm{Var}(\epsilon_j)$ 为定值 $\sigma^2$,也就是 $\mathrm{Var}(\epsilon_1)=\mathrm{Var}(\epsilon_2)...=\mathrm{Var}(\epsilon_i)=\sigma^2$。
把假设 3.1 和假设 3.2 代入 $\mathrm{Var}(\epsilon)$,可得
$$ \begin{equation} \begin{split} \mathrm{Var}(\epsilon) &= \mathrm{E}(\epsilon\epsilon^T)\\ & = \begin{bmatrix} \mathrm{E}(\epsilon_1^2) & \mathrm{E}(\epsilon_1\epsilon_2) & \dots& \mathrm{E}(\epsilon_1\epsilon_i)\\ \mathrm{E}(\epsilon_2\epsilon_1) & \mathrm{E}(\epsilon_2^2) & \dots& \mathrm{E}(\epsilon_2\epsilon_i)\\ \vdots & \vdots & \ddots& \vdots\\ \mathrm{E}(\epsilon_i\epsilon_1) & \mathrm{E}(\epsilon_i\epsilon_2) & \dots& \mathrm{E}(\epsilon_i^2)\\ \end{bmatrix}\\ &= \begin{bmatrix} \sigma^2 & 0 & \dots & 0\\ 0 & \sigma^2 & \dots& 0\\ \vdots & \vdots & \ddots& \vdots\\ 0 & \mathrm{E}(\epsilon_i\epsilon_2) & \dots& \sigma^2\\ \end{bmatrix}\\ &=\sigma^2I \end{split} \end{equation} $$
回到 $\mathrm{Var}(\hat{w})$,这里的 $X$ 视为确定值($X$ 是确定值还是随机变量的讨论后文会提及),所以可以提出来,得
$$ \begin{equation} \begin{split} \mathrm{Var}(\hat{w}) &= \mathrm{E}\big[ (X^TX)^{-1}X^T\epsilon\epsilon^T X(X^TX)^{-1} \big] \\ &= (X^TX)^{-1}X^T\mathrm{E}(\epsilon\epsilon^T) X(X^TX)^{-1} \\ &= (X^TX)^{-1}X^T\sigma^2 I X(X^TX)^{-1} \\ &= \sigma^2 (X^TX)^{-1}X^TI X(X^TX)^{-1} \\ &= \sigma^2 (X^TX)^{-1} \end{split} \end{equation} $$
高斯马尔科夫定理¶
现在我们用反证法来证明 OLS 估计是最佳无偏线性估计,假设存在比 OLS 更好的无偏线性估计 $\tilde{w}$,$M$ 为任意矩阵,设
$$ \tilde{w} = My $$
之所以称之为线性估计,是因为 $\tilde{w}$ 是 $y$ 的线性函数,即 $\tilde{w} = f(y)= My$,OLS 也是 $y$ 的线性函数,即 $\hat{w} = g(y)= (X^TX)^{-1}X^Ty$。
可得 $\tilde{w}$ 的期望是
$$ \begin{equation} \begin{split} E(\tilde{w}) &= E(My) \\ &= E[M(Xw+\epsilon)] \\ &= E(MXw+M\epsilon) \\ &= E(MXw) \end{split} \end{equation} $$
为了使 $\tilde{w}$ 无偏,即 $E(\tilde{w}) = E(MXw) = E(w) = w$,$MX = I$ 必须恒成立。
由于 $M$ 为任意矩阵,我可以将 $M$ 改写为 $(X^TX)^{-1}X^T + C$,$C$ 是任意矩阵。只要 $M$ 存在,我肯定能找到满足 $(X^TX)^{-1}X^T + C = M$ 的 $C$,这里没有任何技术含量,不要想太多。
由于 $MX = I$ 必须恒成立,因此 $CX = 0$,证明如下
$$ \begin{equation} \begin{split} (X^TX)^{-1}X^T + C &= M \\ [(X^TX)^{-1}X^T + C]X &= MX \\ [(X^TX)^{-1}X^T + C]X &= I \\ (X^TX)^{-1}X^TX + CX &= I \\ CX &= 0 \end{split} \end{equation} $$
由于 $\tilde{w}$ 无偏,$MX = I$,$\mathrm{E}(\epsilon\epsilon^T)= \sigma^2I$,可得
$$ \begin{equation} \begin{split} \mathrm{Var}(\tilde{w}) &= \mathrm{E}\big[ [\tilde{w}-\mathrm{E}(\tilde{w})][\tilde{w}-\mathrm{E}(\tilde{w})]^T \big] \\ &= \mathrm{E}\big[ (\tilde{w}-w)(\tilde{w}-w)^T \big] \\ &= \mathrm{E}\big[ [M(Xw+\epsilon)-w][M(Xw+\epsilon)-w]^T \big] \\ &= \mathrm{E}\big[ (M\epsilon)(M\epsilon)^T \big] \\ &= \mathrm{E}(M\epsilon\epsilon^TM^T) \\ &= M\mathrm{E}(\epsilon\epsilon^T)M^T \\ &= \sigma^2MM^T \end{split} \end{equation} $$
由于 $(X^TX)^{-1}X^T + C = M$,$CX = 0$ 以及 $X^TC^T = 0$,因此
$$ \begin{equation} \begin{split} \mathrm{Var}(\tilde{w}) &= \sigma^2MM^T\\ &= \sigma^2[(X^TX)^{-1}X^T + C][(X^TX)^{-1}X^T + C]^T\\ &= \sigma^2\big[ (X^TX)^{-1}X^T[(X^TX)^{-1}X^T]^T + (X^TX)^{-1}X^TC^T + C[(X^TX)^{-1}X^T]^T + CC^T \big]\\ &= \sigma^2\big[ (X^TX)^{-1} + CC^T \big] \end{split} \end{equation} $$
可得 $\mathrm{Var}(\tilde{w}) - \mathrm{Var}(\hat{w})$ 为
$$\mathrm{Var}(\tilde{w}) - \mathrm{Var}(\hat{w}) = \sigma^2\big[ (X^TX)^{-1} + CC^T \big] - \sigma^2(X^TX)^{-1} = \sigma^2(CC^T)$$
因为对于任意矩阵 $A$,$AA^T$ 中的每一项 $\geq 0$ 恒成立(即 $AA^T$ 为半正定矩阵),所以 $\sigma^2(CC^T)$ 中的每一项大于 0,也就是说,$\mathrm{Var}(\tilde{w})$ 中的每一项都大于 $\mathrm{Var}(\hat{w})$,因此比 $\hat{w}$ 更好的无偏线性估计不存在,OLS 估计是最佳无偏线性估计。
假设¶
回顾上面的证明,为了证明 OLS 估计无偏,我们需要假设 1:$\mathrm{E}(\epsilon) = 0$;假设 2:$X$ 为确定值。
为了得到 OLS 估计的协方差矩阵和证明 OLS 估计是最佳无偏线性估计,我们需要假设 3.1:$\forall i \neq j,\ \epsilon_i$ 与 $\epsilon_j$ 独立,$\mathrm{Cov}(\epsilon_i,\epsilon_j=0$;假设 3.2:$\mathrm{Var}(\epsilon_1)=\mathrm{Var}(\epsilon_2)...=\mathrm{Var}(\epsilon_i)=\sigma^2$。这两个假设可以合并为假设 3:$\mathrm{Var}(\epsilon) = \sigma^2I$。
注意,证明 OLS 估计是最佳无偏线性估计不需要假设 $\epsilon$ 呈正态分布。
$X$ 是确定值还是随机变量?¶
在上文的证明里,我们将 $X$ 视作确定值,如果数据来源是可控的实验,$X$ 是实验设计者定义的数值,我给小白鼠甲 1 粒药丸,小白鼠乙 2 粒药丸,小白鼠丙 3 粒药丸... 那么将 $X$ 视作确定值是说得通的,$y = Xw + \epsilon$ 中只有 $\epsilon$ 和 $y$ 是随机变量,其中 $y$ 的随机性只来自于 $\epsilon$。但在大部分情况下,$X$ 是抽样得到的,因此 $X$ 应该视作随机变量,$y = Xw + \epsilon$ 中 $X$、$\epsilon$ 和 $y$ 都是随机变量,$y$ 的随机性来自于 $X$ 和 $\epsilon$,因此假设需要调整,例如假设 1 和假设 2 合并为 $\mathrm{E}(\epsilon | X) = 0$,即样本 $X$ 与误差 $\epsilon$ 不相关(均值独立)的条件下误差均值为零, OLS 估计的期望、协方差矩阵和证明也需要调整,但 OLS 估计是最佳无偏线性估计依然成立,可以参考 Linear regression with random regressors、Regression inference assuming predictors are fixed、Independent variable = Random variable? 以及 Discussion of the Gauss-Markov Theorem。
最小二乘法的局限¶
虽然高斯马尔科夫定理证明了 OLS 估计是最佳无偏线性估计,但是 OLS 依然有局限性。
首先,最大的局限性是其过于看重无偏性。传统统计学理论认为,我们应该先找到无偏估计,再从这些估计里挑选出方差最小的,即便有偏估计的方差比无偏估计的方差更小,因为偏离了真实值,所以没有意义。
虽然传以上说法听起来很有道理,但机器学习领域(尤其是神经网络领域)并不认同这个思路,German et al. (1992) 认为我们应该把偏差和方差综合考虑,即考虑估计的「泛化」能力,这个泛化能力被定义为均方误差(MSE),估计值 $\hat{\theta}$ 与真实值 $\theta$ 的欧式距离,这里的 $\hat{\theta}$ 和 $\theta$ 均为标量,由于 $\hat{\theta}$ 是随机变量,所以将距离取均值,即
$$ \begin{equation} \begin{split} MSE &= \mathrm{E}[(\theta - \hat{\theta})^2]\\ &= \mathrm{E}\big[ [\theta - \mathrm{E}(\hat{\theta}) + \mathrm{E}(\hat{\theta}) - \hat{\theta}]^2 \big]\\ &= \mathrm{E}\big[ [\theta - \mathrm{E}(\hat{\theta})]^2 + [\hat{\theta}-\mathrm{E}(\hat{\theta})]^2 + 2[\theta - \mathrm{E}(\hat{\theta})][\mathrm{E}(\hat{\theta}) - \hat{\theta}] \big] \\ &= \mathrm{E}\big[ [\theta - \mathrm{E}(\hat{\theta})]^2\big] + \mathrm{E}\big[[\hat{\theta}-\mathrm{E}(\hat{\theta})]^2\big] + \mathrm{E}\big[2[\theta - \mathrm{E}(\hat{\theta})][\mathrm{E}(\hat{\theta}) - \hat{\theta}] \big] \\ \end{split} \end{equation} $$
由于 $\mathrm{E}\big[[\mathrm{E}(\hat{\theta}) - \hat{\theta}] \big]=0$,因此
$$ \begin{equation} \begin{split} MSE &= \mathrm{E}[(\theta - \hat{\theta})^T (\theta - \hat{\theta})]\\ &= \mathrm{E}\big[ [\theta - \mathrm{E}(\hat{\theta})]^2\big] + \mathrm{E}\big[[\hat{\theta}-\mathrm{E}(\hat{\theta})]^2\big] + \mathrm{E}\big[2[\theta - \mathrm{E}(\hat{\theta})][\mathrm{E}(\hat{\theta}) - \hat{\theta}] \big] \\ &= \mathrm{Bias}^2(\hat{\theta}) + \mathrm{Var}(\hat{\theta})\\ \end{split} \end{equation} $$
由上可得,估计的均方误差(MSE)可分解为估计的偏差和方差,如果我们让模型更「稳健(robust)」,降低估计的方差,虽然偏差提高,但整体效果也许比无偏估计更好,像是岭回归(Ridge regression)和 LASSO 等就是让模型更「平滑」,取得了比 OLS 更好的泛化能力。这个 rule of thumb 被称为偏差方差取舍(Bias-Variance Tradeoff),但并不意味着提高偏差就一定能降低方差,我们也很难找到 MSE 最低点,它只是方便我们直觉上理解和记忆。
其次,在贝叶斯方法中,最小二乘法只是一种特殊情况,贝叶斯学派预先假设 $w$ 的先验分布来得出 $P(w|X)$ 的后验分布,通过后验分布估计参数得到 $\hat{w}$,这是和频率学派完全不同的思路。
第三,高斯马尔科夫定理的假设可能不满足。对于假设 $\mathrm{E}(\epsilon | X) = 0$,如果 $\epsilon$ 中包括了我们未考虑的变量影响了数据 $X$,或者 $X$ 与 $y$ 相互影响,那么 $X$ 和 $\epsilon$ 不独立,OLS 估计是有偏的,即计量经济学领域研究的内生性问题,需要引入工具变量和 2SLS。对于假设 $\mathrm{Var}(\epsilon) = \sigma^2I$,如果数据是时间序列,$\epsilon_{t1}$ 可能影响了 $\epsilon_{t2}$,即自相关,$\mathrm{Var}(\epsilon) \neq \sigma^2I$ 我们需要使用 GLS 等方法来解决。
最后,高斯马尔科夫定理针对的是线性估计,改用非线性估计也许可以取得更好的效果,例如决策树、随机森林、神经网络、Kernel 等等,线性估计的优势在于计算简单、可以检验显著性(p 值),在计算力和工具高度发达的今天。如果你想要通过数据预测,即解决一个机器学习问题,import scikit-liearn、import keras 再写两行代码就能进行非线性估计,用交叉验证和 Bootstrap 就可以检验模型的泛化能力,万事大吉。但如果你需要用数据检验一个理论(假设)是否正确,检验显著性是必要的,这也是经济学家不喜欢机器学习模型的原因之一。
参考来源¶
频率统计参考了 Dennis D. Wackerly、William Mendenhall III 和 Richard L. Scheaffer 的 Mathematical statistics with applications。
大部分数理统计教科书都没有讨论矩阵方法,只有 John Rice 的 Mathematical statistics and data analysis 讲得比较清楚,我感到沮丧。
机器学习、贝叶斯统计、对频率学派的吐槽,参考了 Kevin Murphy 的 Machine learning: a probabilistic perspective。
均方误差参考了茆诗松的《概率论与数理统计》。
图表引用自 Dennis D. Wackerly、William Mendenhall III 和 Richard L. Scheaffer 的 Mathematical statistics with applications。
修改与勘误¶
- 和我的计量经济学老师 Ioannis Karavias 讨论了 p 值重不重要,得出的结论是,重要。因为目前机器学习尚不能检验对于理论(假设)正不正确,只能得到预测值,可解释性需要打问号。
- 最后一部分证明有误,因为矩阵不能比较大小,需要一些比较 tricky 的方法,不想把证明搞复杂,所以改用半正定矩阵的性质解答。
- MSE 分解为偏差方差的公式中的 $w$ 应该为标量,为了与上面的证明区分,改用为标量 $\theta$。矩阵形式 MSE 分解应该存在,但对结论影响不大,暂时搁置,

本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.